به روز شده در: ۱۷ اردیبهشت ۱۴۰۱
در علم آمار مفاهیمی داریم که ممکنه باهم اشتباه بگریمشون و به جای هم دیگه استفاده کنیم.
- Standard Deviation
- Standard Error
- Confidence INterval
پیش نوشت: هرجا رابطه ریاضی در متن دیدین من اونها رو در قالب لتک نوشتم و مثلا میتونید اینجا پیست کنید و بهتر ببینید شون.
اول به standard deviation میپردازیم.
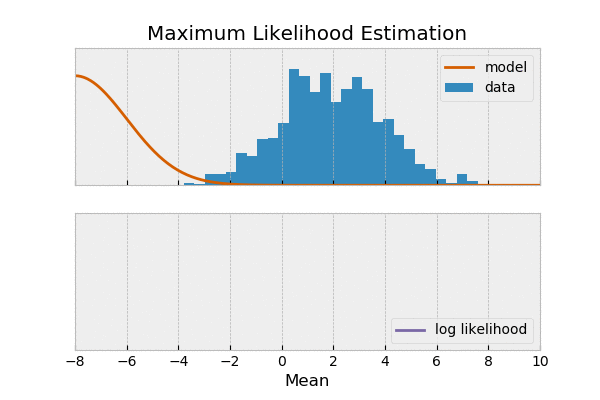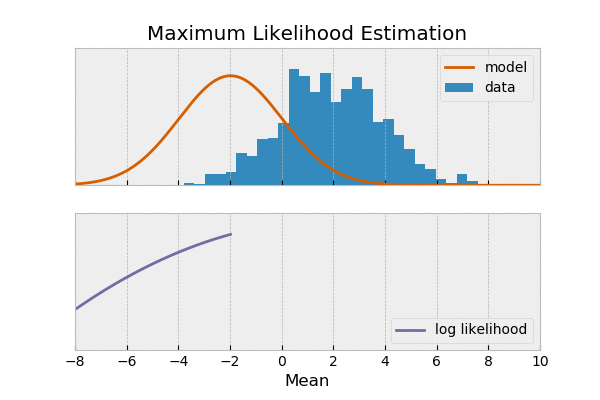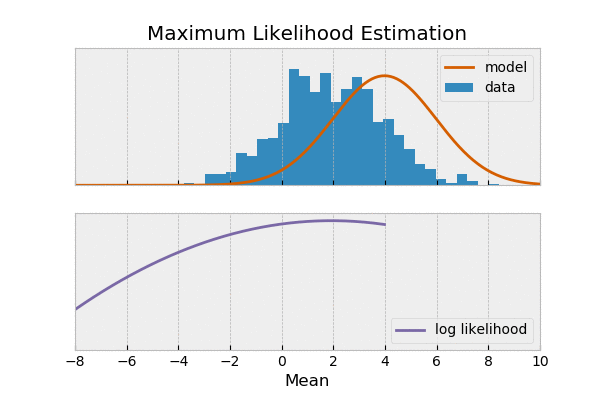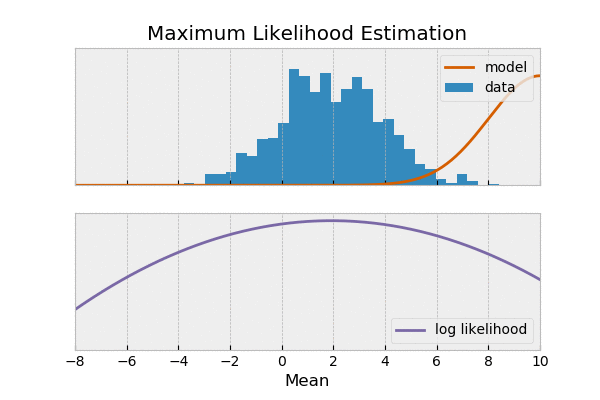
deviation از deviate میاد که اینم اگه برگردیم عقب از de+way = away تشکیل شده. تو فارسی هم بهش انحراف میگن و standard رو هم معیار. و در کل شده انحراف معیار یا انحراف استاندارد. و وقتی ما یکسری مشاده از یک متغیر داشته باشیم میخوایم بدونیم این مشاهدات چقدر پایدارن، آیا هردفعه عوض میشن یا نه یک متر میتونه standard deviation یا به اختصار SD باشه. از این مفهموم برای توضیح دادههامون یا description بکار میره.
انحراف معیار جذر واریانس هست. و رابطش اینطوری حساب میشه.
S.D = \sqrt{\dfrac{(x_i-\bar x)^2}{n-1}}
مثلا اگه اومده باشم از توی باغ سه تا کرم پیدا کرده باشم و طولشون رو با خط کش اندازه بگیرم حاصل این ها شده ۳و۵و۷ سانتیمتر میانگین طول کرمها ۵ سانتیمتر هست و انحراف معیار مثبت و منفی دو سانتیمتر هست. یا اگه طول کرم ها ۴و۵و۶ سانتیمتر میشد میانگین ۵ سانتیمتر و انحراف از معیار مثبت و منفی یک سانتیمتر میشد.
اما Standard Error یا Standard Error of the Mean(SEM) چیه؟
به لحاظ مفهومی یعنی همون میانگین رو احتمالا با چه خطایی اندازه گیری کردیم؟ چقدر میانگینی که اندازه گیری کردیم از میانگین واقعی میتونه دور باشه؟ پراکندگی میانگینها چقدر هست؟
توی زبان فارسی بهش خطای استاندارد یا خطای معیار هم میگن. گاهی میایم کل آزمایش و مشاهداتی که داشتیم رو مثلا ۲۰ بار دیگه تکرار میکنیم که مثلا اگه تو گزارش مون اوردیم میانگین فلان چیز بهمانه بگیم نگا حرف درسته، چون من کل آزمایشم رو ۲۰ بار دیگه هم تکرار کردیم و SD میانگین شده یک عدد کم. جالبه نه؟به عبارت دیگه این دفعه نمونههای من طول کرمها نیستن بلکه میانگینهایی هست که حساب کردم.
حالا خوبیش این هست که لازم نیست شما آزمایشتون رو لزوما n بار دیگه تکرار کنید کافیه با رابطههای که موجود هست میزان Starndard Error یا SE رو گزارش بدین. از این مفهوم نه برای توضیح داده بلکه برای نتیجه گرفتن یا inference از دادهها استفاده میکنیم.
رابطش چیه؟
Standard Error = \dfrac{Standard Deviation}{\sqrt{n}}
سوال: حالا فایدهی خطای استاندارد چیه؟ چه زمانی از SD و چه زمانی از SE استفاده میکنیم؟
فرض کنیم توی سوال من اینه میخوام ببینم طول کرمهایی که تو باغهای هویج هستن با باغی که توش زالزالک کاشتیم تفاوت دارن یا نه؟ مثال دنیای واقعی ترش هم امید به زندگی در افرادی که ورزش میکنند و افرادی که ورزش نمیکنند. حالا من میرم میانگین رو در دو گروه اندازه گیری میکنم. یکی میشه ۷۰ سال یکی میشه ۷۵ سال و در مثال کرم هم یکی میشه ۴ سانتیمتر و اون یکی میشه ۵ سانتیمتر.
حالا میخوام بگم نگاه کنید این دو گروه با هم میانگین ها تفاوت دارن، کمی به این سوال فکر کنید و بعد ادامه مطلب رو بخونید. به نظر شما اینجا باید از SEM یا از SD استفاده کنم؟
بله احتمالا همون طور که حدس زدین برای اثبات حرفم اینجا بهتره از SEM استفاده کنم و بگم ببینم خطای استاندارم کم هست در نتیجه این دو گروه ورزشکار و غیر ورزشکار از هم واقعا تفاوت دارن ولی SEM طول کرمها زیاد شده و در نتیجه طول کرم ربطی باغ هویج یا زالزالک نداره.
توجه داشته باشین همیشه طول SE از طول SD با یک ضریب رادیکال n کوچکتر هست. به عبارتی SD که تون رو حساب کردین تقسیم بر ردایکال اِن کنید میشه طول SE تون.
بازه اطمینان یا Confidence Interval
اگر بیایم و همون SE رو در ۱.۹۶ ضرب کنیم(همون تقریبا دو برابر کنیم) حالا ما به بازه اطمینان رسیدیم. بازه اطمینان به ما چی میگه؟ میگه اگر بیایم آزمایش مون رو بینهایت بار تکرار کنیم با احتمال ۹۵ درصد میانگین واقعی مون طوی بازه اطمینان میوفته.
اگر در یک آزمایش ببینیم بازه اطمینان دو حالت باهم تفاوت داره، میتونیم نتیجه بگیرم که این تفاوت به احتمال ۹۵ درصد معنی داره (یعنی p-value < 0.05) هست. و اگه بازه اطمینان دو حالت با هم اشتراک داشت یعنی p-valuse مون بیشتر از پنج صدم هست و این اختلاف دیده شده معنی دار نیست.
بیشتر بدانید:
قانون ۶سیگما چی میگه؟ میگه بیاد SD تو حساب کن طول error bar تو ۶برابر کن سه تا بیا بالا و سه تا هم پایین. حالا به احتمالا ۹۹ درصد تک تک نمونههای تو در این بازه میفتن.
take home message:
اگر مهم اینکه من چه نمونههایی دیدم و چه نمونهایی خواهم دید از SD استفاده کنیم ولی اگه خواستیم بگیم میانگین دو چیز با هم متفاوتن بهتره از SE استفاده کنیم.
منبع(+)