فیت کردن یک خط به دادهها
به روزرسانی ۲۶امرداد۱۴۰۰
این فیلم رو هم آماده کردم که میتونید ببینید.
در ادامه مطلب به این میپردازیم که چطور داده هامون رو با یک خط بیان کنیم.
پس بیاین عبارت مشابهی که به این منظور استفاده میشن رو با هم بشناسیم تا از این به بعد هرجا دیدیمشون بدونیم از چی دارن حرف میزنن:
- Linear regression
- Least squres optimization
- Fitting a line to data
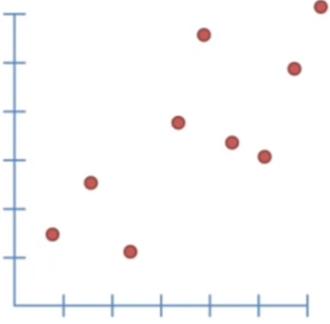
فرض کنید یک سری داده جمع کردین مثل اینها
تصویر۱: دادههای ما مثل محور افقی میتونه پول باشه و محور عمودی آش دریافت شده (هرچقدر پول بدی همونقدر آش میخوری)
و حالا ما میخوایم یک خط رو روی اینا فیت(براز/نگاشت) کنیم ببینیم ترند(روند) دادهها چطوریه، سوالی که مطرح میشه این هست که خوب کدوم از همه بهتره؟
تصویر۲: کدوم خط بهتر از همه نماینده داده هاست؟
میتونیم بیایم فاصله تک تک نقاط رو از خط حساب کنیم هرچی این جمع فاصله ها بیشتر باشه یعنی خطی که انتخاب کردیم خوب نبوده و برعکس اگه مجموع این فاصلهها عدد خیلی کوچیکی بشه یعنی خط خوبی پیدا کردیم.
تصویر۳: اگه ما بخوایم ببینیم خط افقی سیاه رنگ با عرض b چقدر خوبه میتونیم بیایم فاصله شو از تکتک نقطهها حساب کنیم و با هم جمع کنیم.
حالا اگه دقت کنید متوجه میشین که نقطههایی که زیر خط هستن فاصله شون یعنی b - y_i ( نماد b همون عرض خط هست و نماد y_i نماد عرض نقطه i ام و آندرلاین مثل دستورات لاتک یعنی اندیس) یک عدد مثبت میشه ولی برای نقطه های بعدی که بالای خط هستن این فاصله یک عدد منفی میشه، و وقتی خواستیم کل فاصلهها رو باهم جمع کنیم این کار رو خراب میکنه، شاید بگین بیا و از قدر مطلق استفاده کن یعنی |b - y_i| ها رو باهم جمع کن، پیشنهاد خوبی هست ولی مثل اینکه قدرمطلق حساب کتاب رو در آینده کمی پیچیده میکنه راه دیگه به توان دو رسوندن فاصله هست، بیایم و فاصله رو مربعش کنیم یعنی 2^(b - y_i) رو حساب کنیم (اینجا هم علامت هَت ^ مثل لاتک یعنی بالا اندیس).
حالا که ما اینجا ۹ تا نقطه داریم باید حاصل این عبارت رو حساب کنیم.
(b-y1)2 + (b-y2)2 + (b-y3)2 + (b-y4)2 + (b-y5)2 + (b-y6)2 + (b-y7)2 + (b-y8)2 + (b-y9)2
و فرض کنید حاصلش برای این خط افقی شده ۳۰، به این حاصل میگن مجموع مربعات باقیماندهها یا همون sum of squared residuals
نظرتون چیه یکم این خطو بچرخونیم ببینیم جمع این حاصل چه تغییری میکنه؟
تصویر۴: یک خط دیگه و فاصلههای جدید اگر برای sum of sequared residual رو حساب کنیم مثلا میشه ۱۵
حالا اگه قبول داشته باشین یک خط رو میشه با y = ax + b نشون بدیم به a میگیم شیب خط (slope) و به b میگیم عرض از مبدا خط (intercept) و ما باید بهترین خط که کمترین فاصله رو داشته باشه پیدا کنیم به عبارت دیگه a,b بهینه رو پیدا کنیم. (Minimizing sum of squared resiudals)
((ax1+b) - y1)2 + ... + ((ax9+b) - y9)2
this equation sayes sum of squared residual(line - point)
تصویر۵: نمودار پیدا کردن پارامتر های بهینه محور افقی داره میزان چرخش خط و محور عمودی داره مجموع مربعات باقیمونده رو نشون میده.
خب خب خب، یک سوال مهم نقطه بهینه رو چطور پیدا کنیم؟ کافیه مشتق این تابع رو حساب کنیم و اگر موافق باشید مشتق هر تابع در یک نقطه داره شیب اون نقطه رو نشون میده به عبارت دیگه میگه اگه یک کوچولو x رو زیاد کنی y چقدر زیاد میشه حالا باید بگردیم ببینیم کجا شیب تابع یا همون مشتقش صفره.
نکتهای که هست معمولا کسی این مشتق و پیدا کردن مقدار همزمان بهینه شیب و عرض از مبدا رو به صورت دستی پیدا نمیکنه و برای این کار از کامپیوتر استفاده میکنن.
حالا که خطو پیدا کردیم میتونیم بگیم این خط least squares هست.
پ.ن: خیلی دوست دارم جزئیات مشتق حساب کردنش رو اینجا بیارم ولی فرمول نوشتن مثل اینکه سخته باید یک حرکتی بزنم یا توی pdf بنویسم یا تو فایل جوپیتر نوتبوک فعلا که ایدهی راحتتری ندارم.
منبع آموزش (+)