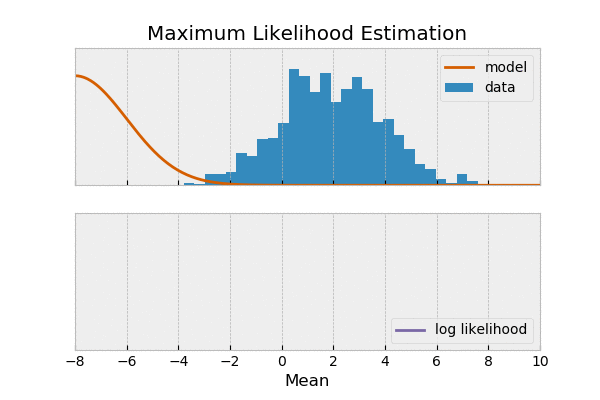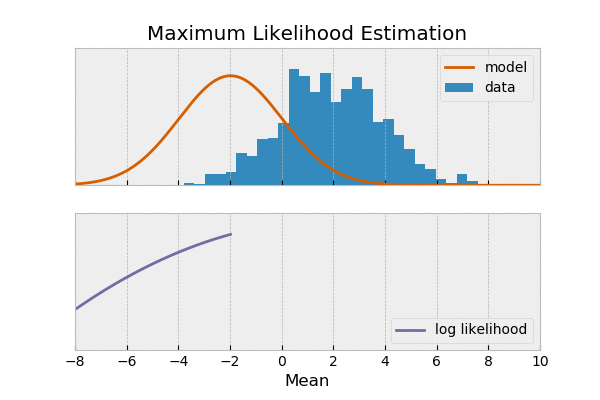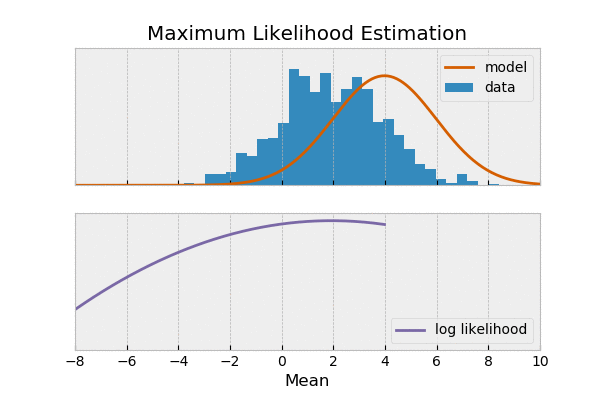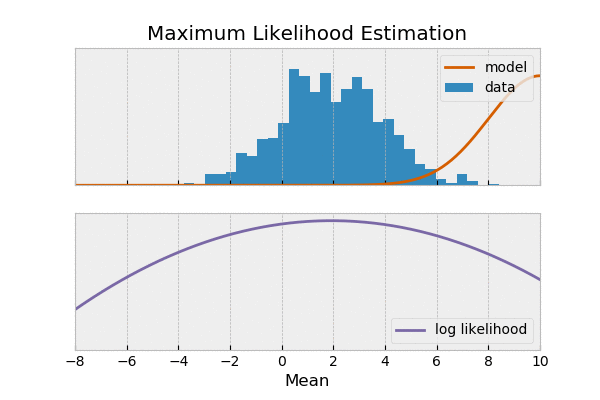
Probability Vs Likelihood
یک وقت هست شما میخوای بدونی سکه که میندازی شیر میاد یا خط، میگی احتمال شیر اومدن ۰.۵ هست. بعضی وقتها نه کلی داده جمع کردی از پرتاب یک سکه میخوای ببینی آیا سکه سالم بوده؟ یعنی احتمال شیر اومدن ۰.۵ بوده اون وقت میری سراغ تابع درستنمایی یا لایکلیهود. به عبارت دیگه در حالت اول دنبال پیش بینی آینده هستی و در حال دوم دنبال پیدا کردن مدل.
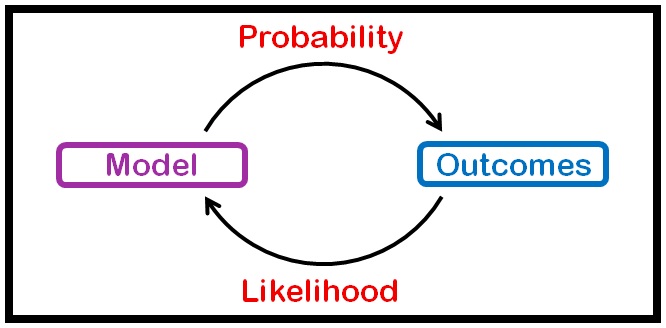
مثال: فرض کنید شیرین و ملیحه آشپزی کردن شیرین دوست داره غذای های شکری درست کنه و ملیحه هم دوست داری غذاهای نمکی درست کنه. دیشب شیرین، فالوده درست کرده ملیحه هم نودل،
در حالت احتمال شما مدل رو داری یعنی مثلا شیرین پیشته و سوالت این هست که چقدر احتمال داره شیرین یک غذای شور درست کنه
ولی در حالت لایکلی هود یک مشاهده داری یعنی مثلا غذا رو دیدی یا خوردی مثلا نودل رو حالا سوالت اینه که چقدر احتمال داره دست پخت شیرین باشه؟
تو اینجا شیرین و ملیحه همون مدل هستن و غذاهاشون داده.
مثال: سنجش میگه ۶۰ درصد کنکوریها خانم و ۴۰ درصد آقا هستن(مدل یا جامعه من). حالا من میرم دوربین ورودی دانشگاه رو میبینم برای یک ساعت(نمونه یا داده من). احتمال اینه که بگیم نسبت خانم و آقا در دوربین چیه؟ ولی یک وقت هست کار پیچیده تره و من به مدل یا جامعه دستری ندارم، مثلا بهداشت میگه ما از شهر چابهار ۱۰۰ نمونه کرونا گرفتیم و دیدیم ۱۰ نفر مبتلا هستن. حالا چقدر احتمال داره نصف شهر درگیر باشن؟ این سؤال دوم که از نمونه میخوایم برسیم به جامعه از جنس لایکلیهود هست.
چند تا نکته راجع به نحوه نوشتن:
- X = Random variable
- x = a sample
- L = Likelihood function
- Parameter = What machine find
- Hyper-parameter = What you set
- θ = Distribution or distribution parameter
- Probability
- is function of x
- is area under PDF(probability density function)
- about future event
- attaches to possible results
- Likelihood is
- function of θ
- point on PDF
- usally abut past event
- attaches to hypotheses
- L(θ|x) = P(x|θ)
- Sum of the P is 1
- Sum of the L is not necessary 1
- L maybe continues and P discrete
مطالعه بیشتر (+)